Grayscale Morphology

date:Jul 18, 2007

What is grayscale morphology?

If you are not familiar with binary morphology, you may want to read about it first. As mentioned in the section on binary morphology, grayscale morphology is simply a generalization from 1 bpp (binary) images to images with multiple bits/pixel, where the Max and Min operations are used in place of the OR and AND operations, respectively, of binary morphology. The following should be noted:

• These operations, as with binary morphology, are nonlinear. The significance of nonlinear operations, as opposed to linear operations, is that nonlinear operations can be used directly for making decisions about regions of the image. Nonlinear operations are therefore of particular use in image analysis.

• The generalization can be seen in reverse: binary morphology is a specialization of grayscale morphology. The Max of a set of values {0, 1} is equivalent to an OR, and the Min is equivalent to an AND.

• The generalization only applies to flat structuring elements. With grayscale images, dilation and erosion can be defined with non-uniform structuring elements. These are rarely used, and will not be discussed further.

• With flat structuring elements, grayscale morphology is itself a specialization of rank-order filters. When a rank-order filter acts on a source image, it generates a dest image where each pixel is computed as follows: place the structuring element with its origin on the corresponding source pixel, and choose the rank (ordered) pixel in the set of source pixels that is covered by the structuring element. Erosion is thus a rank-order filter with rank = 0.0; dilation has rank = 1.0; and the median filter, which is useful for removing noise, has rank 0.5. (To be completely accurate, when doing a dilation as described here, invert the structuring element about its origin.)

• Because the standard photometry of binary and grayscale images is opposite (white is min val in binary and max val in grayscale), grayscale dilation lightens a grayscale image and erosion darkens it, visually.

• Without special hardware registers that do Min and Max comparisons on 4 or 8 bytes simultaneously, grayscale morphology must be done by comparing integers, one pixel at a time. It is thus much more than 8 times slower than implementations of binary morphology that pack 32 pixels into each 32-bit word.

• This inefficiency is somewhat offset by the existence of a simple algorithm that computes grayscale morphological operations in a time independent of the size of the structuring element.

For the general case of an arbitrary SE of size A, where A, the “area” of the SE, is the number of hits, the computation of the Max or Min requires A pixel comparisons on the src image for each pixel of the dest. However, things get more efficient when the SE is a brick, by which we mean it is a solid rectangle of hits. For a brick SE, dilation (or erosion) can be decomposed into a sequence of 2 dilations (or erosions) on 1-D horizontal and vertical SEs. Each 1-D grayscale morphological operation can be done with less comparisons than the “brute-force” method. Luc Vincent described one such method, that uses an ordered queue of pixels, given by the set of pixels currently under the SE. The queue is ordered so that the Min or Max can be read off from the end. When the SE is moved one position, one pixel is removed from the queue, and a new pixel is placed into it, in the proper location. Most of the work goes into sorting the queue to maintain the order.

More recently, van Herk, Gil and Werman have described an algorithm that uses a maximum of 3 comparisons for a linear SE, regardless of the size of the SE. This method is described below, and it is the method we have implemented here.

Some useful image transforms are composed of a sequence of grayscale operations. For example, the tophat operator is often used to find local maxima as seeds for some filling operation. It is defined as the difference between an image and the opening of the image by a structuring element of given size. Another local maximum finder is called the h-dome operator, and it uses a grayscale reconstruction method for seed filling. (Yes, with h-domes, you do a seed-filling operation to find seeds for another operation!). These are discussed in detail in the section on tophats and h-domes below.

Implementation using the van Herk/Gil-Werman algorithm

The van Herk/Gil-Werman (vHGW) algorithm is similar to our fast method for convolution with a flat kernel, where we first computed an accumulation matrix and then used it to quickly generate the convolution for any rectangular kernel. vHGW differs in that we compute a localized running Max (or Min) array that is specific to the size of the linear SE, and we then use the array to compute the result pixels locally (over a length equal to the SE size).

The vHGW algorithm was published by van Herk in A fast algorithm for local minimum and maximum filters on rectangular and octagonal kernels, Patt. Recog. Letters, 13, pp. 517-521, 1992 and by Gil and Werman in Computing 2-D min, median and max filters, IEEE Trans PAMI, 15(5), pp. 504-507, 1993. (There appears to be some priority dispute, so I take a neutral position and give credit to both sets of authors.) This was the first grayscale morphology algorithm to compute dilation and erosion with complexity independent of the size of the SE. It is simple and elegant, and the surprise is that it was only discovered as recently as 1992. It works for SEs composed of horizontal and/or vertical linear elements, and requires not more than 3 pixel value comparisons for each output pixel. The algorithm has been recently refined by Gil and Kimmel, in Efficient Dilation, Erosion, Opening and Closing Algorithms, given at ISMM (International Symposium on Mathematical Morphology) 2000, Palo Alto, CA, June 2000, and was published in Mathematical Morphology and its Applications to Image and Signal Processing, Kluwer Acad. Pub, pp. 301-310. They bring the number down below 1.5 comparisons per output pixel, at a cost of significantly increased complexity. Consequently, we’ll describe and implement the original method.

We describe dilation; for erosion, substitute Min for Max. In brief, the image is divided into pixel groups of length L, where L, an odd number, is the size of the SE. We describe the case for a horizontal SE with its origin at the center position (L/2). Vertical SEs are handled similarly, except the pixels are selected in vertical groups. On each raster line of length w, we compute output pixels starting at x = L/2 (to avoid boundary effects) and operate on N = (w - 2 * (L/2))/L segments of length L. N takes this particular form to avoid boundary effects on the right side as well, so that the last segment of length L is guaranteed to have the SE entirely within the image at all L points. As a result, we do not evaluate the first L/2 pixels and, in the worst case, the last 3L/2 pixels. To get reasonable results on all pixels in the image, we embed the actual image in a larger image with these augmented dimensions, where the added border pixels are appropriately initialized (to 0 for dilation and to 255 for erosion). The algorithm proceeds for each group of L pixels in 2 steps. In the first, we form the running Max array; in the second, we evaluate the output pixel values.

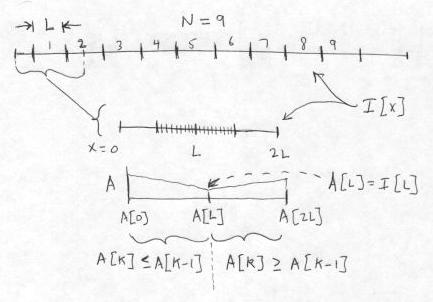
For each group of L pixels, we consider a window of 2L+1 pixels in the source image that extends L/2 pixels to either side. The pixel at the center of the L pixels is also at the center of this larger window. Form an array A[] of length 2L+1, consisting of backward and forward running Max pixel values, which are computed starting at the source pixel at the center of the group of L pixels. This array will coincide with the larger window of 2L+1 pixels. Now, consider the very first group in the raster. The larger window starts at the left edge (x = 0) and proceeds to x = 2L. The center value of the Max array, A[L], is given by the pixel at x = L. The value to the left of that, A[L-1], is given by the Max of the values of the pixel at x = L and the pixel at x = L-1, and so on progressively to the value at the beginning of the array, A[0], which is the Max of all pixels from x = L back to x = 0. The array values to the right of A[L] are likewise found by taking the Max of all pixels from x = L up to that point, progressing finally to the value at the end of the array, A[2L], which is the Max of all pixels from x = L to x = 2L. In all, this step requires computing 2(L-1) Max functions.

The generation of the running Max array A[] from the source image I is shown below. We display the domain over which a raster line of the image I is defined, but we do not display I[x] itself. As shown, there are N=9 pixel groups of length L for which output pixels can be computed. We magnify the first interval of length 2L+1 in I. This covers the relevant pixels in I that are used for generating the first pixel group of L output pixels in I\’:

Once this array is formed, the values of the dilated pixels, that are written to the destination image, can easily be read off. For this first interval of length L, the L output image pixels from x = L/2 to x = 3L/2 are computed by imagining that the SE is placed on the array A with its center at one of these L locations; namely, at each pixel for which the SE fits entirely within the array A. We start at x = L/2, where the end points of the SE are at x = 0 and x = L, and take the Max(A[0], A[L]) = A[0]. (We know here that A[0] >= A[L], by the construction of the array A.) Then at x = L/2 + 1, we take Max(A[1], A[L+1]), and so on, up to the last value at x = 3L/2, which is Max(A[L] + A[2L]) = A[2L], again by construction. In all, this step requires computing L-2 Max functions.

The method for computing the destination (dilated) pixel values I\’[J] from the source image I, for the first pixel group given by L/2 <= x <= 3L/2, is shown below. The computation of the output pixel at x = J is shown explicitly.

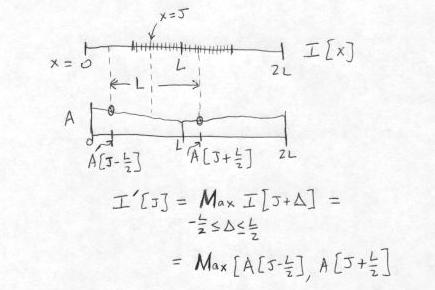
The total number of comparisons per output pixel is 3 - 4/L, which is never greater than 3. The calculation described above is repeated at each of the N segments of length L on the raster line.

The implementation is straightforward. We set up two buffers, one to hold an entire raster line (or column, for vertical SEs) of the image, and the second to hold the running Max(Min) array of size 2L+1. The raster line buffer is used to hold the pixels in byte order. For little-endian machines, this is exactly opposite to the standard pixel order for 32-bit words, which puts the pixels in MSB-to-LSB order; i.e., 3, 2, 1, 0. The pixel order in each 32-bit word is reversed as pixels are copied to the buffer. (For big-endian machines, no pixel reshuffling is necessary.) For vertical SEs, we just take the pixels in a column in order from top to bottom. See the source code in graymorphlow.c for other details.

As with binary morphology, opening and closing are defined as a sequence of erosion/dilation and v.v. These operations are idempotent, so one simple test for correctness is to open an image with a SE and then open the result. The second opening should give the same image as the original one. Our implementation permits morphological operations with SEs that are linear (horizontal or vertical) and square (implemented as a sequence of horizontal and vertical operations). The speed is independent of the size of the SE and proceeds at about 120 P3 machine cycles per output pixel, for large images.

The Tophat and H-dome transforms

The tophat transform is a composite operation that uses the morphological opening or closing. The h-dome transform uses grayscale reconstruction. Both give local extrema (minima and maxima) in grayscale images that can be used as seeds in a segmentation algorithm. To motivate the use of these image transforms as generators of seeds, we give a quick review of segmentation here.

Binary segmentation most simply is carried out by selecting connected components in the image, using a seed image, a mask image (which is typically the actual image), and filling selected connected components in the mask that have seeds in them. Here, the mask is used to clip the filling process. In a more complicated situation, typified by a binary image of touching coffee beans, you need to split binary connected components. This can be done using the distance function and looking for low saddle points that are most easily cut through. How do you do that? Put the distance function upside-down. Then the seeds, which are the local maxima of the distance function (the points that are farthest from the boundaries) are at the bottom of the inverted function. The boundaries are at the highest point, and the “low passes” through the saddle are on the boundaries of the catchment basins. Segmentation is achieved by filling the basins to define the watersheds, which are all the points that drain into the same basin.

Similarly, grayscale segmentation usually proceeds by finding markers, or “seeds,” and an image of catchment basins surrounded by walls at the boundaries. The catchment filling “mask” can be computed in various ways; a popular one is to use a properly smoothed morphological gradient, which has large peaks at places where the image intensity is rapidly varying — a likely position to find a segmentation boundary. Filling then proceeds from the seeds into these basins.

There are various ways to get the seeds. Two popular ones are tophat and h-dome transforms. The tophat is simpler, and you can envision its operation as follows. Suppose you have a dark grayscale image with some small bright regions. To identify those regions, apply the tophat, using a SE that is larger than the extent of the regions. The opening is a Min operation that removes those bright regions that are smaller in dimension than the SE used in the opening. Then, subtracting this image with the thin peaks cut off from the original image gives you just those peaks, plus some low amplitude noise. The tophat is typically followed by a thresholding operation on the peaks. We’ve just described the white tophat. There is a black tophat that is a dual to the white tophat, and it subtracts the original image from the closing with a SE. The black tophat gives large pixel values in the result where there were small dark regions in the original image.

The h-domes are another method for finding local maxima. They use a grayscale reconstruction (seed filling) method, where the original image is the mask and the seed is derived from the mask by subtracting a constant value “h” from each pixel value. Reconstruction expands the seed into the original image (mask). This is visualized as having each local maximum of the seed expand horizontally until it hits a value of the mask that is of equal or greater value, at which point it can expand no further. To complete the h-dome transform, the filled seed is then subtracted from the original image, resulting in an image composed of the “domes” of local maxima of the original, none of which can exceed the value h in size.

You can find implementations of the tophat transform pixTophat() and the hdome transform pixHDome() in morphapp.c. We have implemented both black and white tophat transforms, even though they are trivially related. Intuitively, applying a black tophat to find small dark regions should be equivalent to applying a white tophat to the inverse of the image. (The inverse of an image is found by replacing each pixel by its reflection in the light-dark axis; specifically, if the pixel has value v, it is replaced by the value 255 - v.) And, in fact, this is correct. These operations have exactly that simple duality relation: the white tophat on an image is equal to the black tophat on the inverse of the image, and v.v. The proof, which uses the duality of the opening and closing operations, is very simple. Let the opening of an image I with a structuring element S be given by O_s(I), and the closing of I by S be C_s(I). From here on, due to a typographic limitation of HTML, we’ll suppress the “S”. Denote the inverse of an image I by I, where I = 255 - I. The opening and closing are dual, in the sense that O(I) = C(I). (Note that this is a different sense of “dual” than for the black and white tophats, which we are in the process of showing.) Denote the white tophat by Tw(I) = I - O(I) and the black tophat by Tb(I) = C(I) - I. Then the black tophat on the inverse of I is given by:

Tb(I) = C(I) - I = O(I) - I = 255 - O(I) - 255 + I = I - O(I) = Tw(I)

which is the result that was to be proven. By the way, the duality relations for opening and closing, O(I) = C(I), or C(I) = O(I), can be stated in words in several ways. Here’s one for the second of the pair: The closing of an image can be equivalently found by inverting the opening of the inverted image. This holds for binary as well as grayscale, of course.

High frequency noise, which is not well filtered by the white tophat, can be greatly reduced by doing a closing first. Likewise, an opening is often necessary before a black tophat. The size of the SE in the opening or closing can be comparable to that used in the tophat.

(Parenthetical note. For seeing the results clearly, we provide a function pixMaxDynamicRange() that expands the dynamic range to cover the full set of 256 values for an 8 bpp image. We let you do this with either a linear or log transform. The latter is useful for images that cover a large dynamic range to begin with and have small values that you wish to see and which appear black on a linear scale.)

Generalization: rank order filters

Definition

For simplicity and implementation efficiency, we consider only brick (rectangular: wf x hf) filters. A brick rank order filter evaluates, for every pixel in the image, a rectangular set of n = wf x hf pixels in its neighborhood (where the pixel in question is at the “center” of the rectangle and is included in the evaluation). It determines the value of the neighboring pixels that is the r-th smallest in the set, where r is some integer between 1 and n. The input rank is a fraction between 0.0 and 1.0, where 0.0 represents the smallest value (r = 1) and 1.0 represents the largest value (r = n). A median filter is a rank filter where rank = 0.5. The rank order filter is a generalization of grayscale erosion and dilation. The erosion is equivalent to rank = 0.0 (because we’re choosing the minimum in the set), and a dilation is equivalent to rank = 1.0 (the maximum). The min and max are much easier to calculate than the general rank value, thanks to the van Herk/Gil-Werman algorithm. The brick grayscale erosion and dilation are separable, which also increases the efficiency of implementation, whereas the general rank order filter is not. In our implementation, if these extremal ranks are specified, and the filter dimensions are both odd, the appropriate separable morphological operation is dispatched by the rank order function pixRankFilterGray().

How is a brick rank order filter implemented efficiently?

The brute force method is to sort all the neighboring pixels, and pick the value of the r^th one. The best sorting algorithms are O(n*logn), where n, the area of the filter, is the number of values to be sorted. For a 50x50 filter, the number of operations at each pixel is over 10,000, which is not practical. (These are not machine operations.)

However, we only need the r-th largest pixel. So our problem is really a “selection” one (e.g., quickselect), not a sorting problem. Now it turns out that using a variation of quicksort, selection of any specific rank value is O(n). This is because for selection you only need to sort the appropriate segment at each bifurcation in the quicksort method, rather than the entire tree. (For details, see Numerical Recipes in C, 2nd edition, 1992, p. 355ff.) There is a constant 2 in front of the n, relative to quicksort, so this brings the count down to 5,000 for our example, which is still ridiculously large.

Actually, we only need to do an incremental selection or sorting, because moving the filter down by one pixel causes one filter-width of pixels to be added and another to be removed. Can we do this incrementally in an efficient manner? Perhaps, but I don’t know how. The sorted values will be in an array. Even if the filter width is 1, we can expect to have to move O(n) pixels, because insertion and deletion can happen anywhere in the array. By comparison, heapsort is excellent for incremental sorting, where the cost for insertion or deletion is O(logn), because the array itself doesn’t need to be sorted into strictly increasing order. The heap, which is represented by an array, only needs to be in “heap” order, so just a few elements must be rearranged. However, heapsort only gives the max (or min) value, not the general rank value.

The conclusion is that sorting and selection are far too slow. All is not lost, because we can still use a histogram of pixel values. But how is this to be represented?

Suppose we represent the histogram as an array of 256 bins, which is the usual situation. At each new filter location, the histogram must be updated and the rank value computed. The problem we face is that, in general, to find the rank value, a significant fraction of the entire histogram must be summed. Suppose the filter size is 5x5. There are at most 25 different bins occupied, and we will mostly be adding zeros to the sum of bin occupancies. That is painful!

We can instead use a linked list, so that there won’t be any unoccupied cells and the sum can be quickly done. However, we lose random access for insertion and deletion, so those operations become unacceptably slow.

However, we can mostly overcome the empty bin problem and retain random access by using two histograms represented as arrays, with bin sizes 1 and 16. Each of these histograms is updated for each pixel added or removed when the filter is moved. To find the rank value, proceed from coarse to fine, first locating the coarse bin for the given rank value, of which there are only 16. Then for the fine histogram with bin size 1 and 256 entries, we need look only at a maximum of 16 bins. On average, there will be a total of about 16 sums.

Points of interest in the implementation

The implementation is in rank.c. There are several things to notice:

• Two histograms are maintained throughout: a 16-bin coarse histogram and a 256-bin fine histogram, as mentioned above.

• The histograms are updated incrementally, using either row major order or column major order, depending on the aspect ratio of the filter. For row major order, which is used when the filter height hf is larger than the width wf, the fast scan is down the column. For that case, for each column, generate the histogram for the entire filter at the first location (the top of the column). Then as the filter is moved down, remove the values for the old top row and add the values for the new bottom row.

• Avoid special-case processing for pixels near the boundary by expanding the image by half the filter dimension on each side (specifically, half the horizontal dimension on left and right sides, and half the vertical dimension on top and bottom).

• To avoid bias as far as possible in the added boundary pixels, we mirror the pixel values across the boundary.

• For convenience, choose the filter “origin” implicitly at the UL corner. Then we can simply march through dimensions of the width and height of the original (un-bordered) image to generate the destination (rank-order) image.

• If both filter dimensions are odd and the rank is either 0.0 or 1.0, we use instead grayscale erosion or dilation, respectively. The reason both dimensions have to be odd is that grayscale erosion and dilation are only computed using filters of odd width and height.

• If the input rank is 0.0 or 1.0, with at least one filter dimension being even, it is necessary to use the slower rank order function. However, we move the rank value slightly off the input value (e.g., move 0.0 to 0.0001) to allow use of a simpler comparison in the inner loop that does the sum over histogram bins.

The operation is reasonably fast, considering its complexity. The speed is essentially independent of the size of the larger dimension of the filter. The time is approximately a constant plus a term that is linear in the smaller dimension of the filter (generated by prog/rank_reg.c). In the figure below we show the operation time per Mpixel vs the smaller filter dimension.

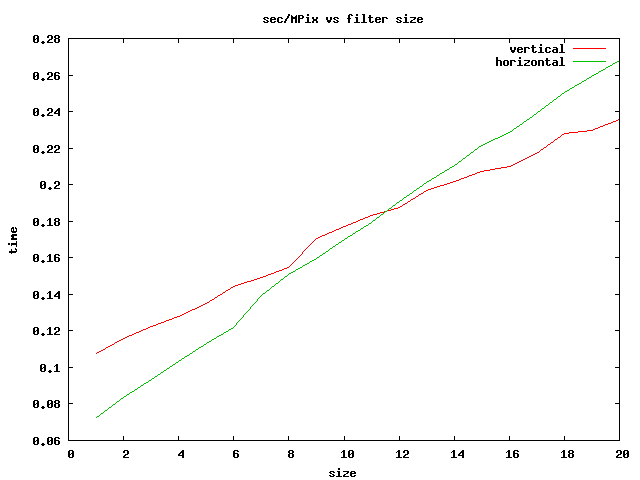
Note that a rank operation with a horizontal filter is faster than with a vertical filter when the small dimension is very small, but the incremental increase in time as the small dimension expands is larger for the horizontal filter. The latter effect can be understood because for the horizontal filter, the incremental pixel addressing is over two vertical columns, which is slower than addressing across two rows. For a moderate sized filter with a smallest dimension of 20, the rank order filter operates at about 4 MPix/sec on a 3 GHz machine. If you can speed this function up significantly, please let me know.