Image Scaling

date:Sept 21, 2008

Overview of image scaling

Image scaling is important for many situations in both image processing and image analysis. Consequently, a number of different scaling functions are provided in Leptonica.

Binary images at high resolution (300 to 400 ppi) can be used to make low resolution binary images for analysis or display on a low resolution device (such as a monitor). To make a version of a page image that is readable on a grayscale display, the scale-to-gray function can be used to produce a grayscale image (of at least 4 bpp) at about 100 ppi. Scale-to-gray can also be used to convert a binary image to a very low resolution grayscale page icon thumbnail at about 15 ppi. At such resolution, a 10 x 7 inch image shrinks to 150 x 105 pixels, which appears on a 100 ppi high resolution monitor as an icon of size 1.5 x 1.05 inches.

When scaling a grayscale or RGB color image, two things must be kept in mind. First, if the image is significantly reduced, it is useful to first apply a lowpass filter whose size is roughly the same as the subsampling factor, in order to reduce aliasing. Second, if the image is significantly enlarged, it is useful (though more expensive) to apply a linear interpolation to the original image, in order to avoid constructing blocks of equivalent pixels that are visibly “jagged” when simple pixel replication is used.

Finally, there is the upscale-to-binary operation, in which a grayscale image is upscaled to a higher resolution binary image. This is the inverse of scale-to-gray, and can be thought of as an example of image restoration; namely, restoring a higher resolution binary image, that had been previously downscaled to gray. We don’t provide any estimation routines for this explicitly, but the operation can be performed with good results by a succession of two operations: grayscale upscaling using linear interpolation, followed by binarization using a threshold or dithering. (We provide several efficient composite operations of these types.)

Aliasing occurs when a signal is (sub)sampled at less than twice the wavelength of the highest frequency. To avoid aliasing, the high frequencies in the signal are removed with a lowpass filter before sampling. The sinc filter is ideal in that its representation in the fourier domain has constant value up to the cutoff frequency, where it goes to zero. Thus, it will remove aliasing with the smallest amount of blurring of the result. However, the sinc has infinite extension, and is impractical for efficient image processing. For our purposes, a reasonable compromise between acceptable blur and computational efficiency is to use a constant height convolution filter. The function pixBlockconv() has a computational time independent of the size of the filter, and is used for some of the lowpass filtering.

We enumerate and comment on these (four) operations in the next section, and then go into detail after that. See the table at the end of this page for an overview.

What types of image scaling are useful?

Note: in the following, when we refer to grayscale images, we intend to include color images as well. The color images used in Leptonica are either colormapped grayscale (where each gray value refers to a specific RGB color), or they are full 24 bpp RGB images. Likewise, the images in Leptonica that are strictly grayscale are either colormapped grayscale (where each RGB value in the colormap is actually gray, with R=G=B), or grayscale without a colormap. RGB images can be handled as three separate 8 bpp grayscale component images. Leptonica provides functions for separating the component images out so they can be processed as grayscale 8 bpp images, and combining the components back to form a color RGB image. Some of the fastest color operations do not perform this separation, but instead operate on the R, G and B components in situ, pulling them out of the 32 bit pixels and replacing them after the operations are completed. Leptonica also provides functions for converting a colormapped 2, 4 or 8 bpp image to grayscale or full RGB color images. For all scaling operations except simple subsampling or pixel replication, it is necessary to convert a colormapped image to either grayscale or full RGB before applying the scaling operation.

There are four main classes of image scaling:

1. grayscale –> grayscale

2. binary –> binary

3. binary –> grayscale (typically downscaling)

4. grayscale –> binary (typically upscaling)

Class 1 (grayscale –> grayscale) can be done crudely by sampling, or more accurately by low-pass filtering followed by sampling, by area mapping, or by resampling with linear interpolation. The issues are explored in detail below.

Class 2 (binary –> binary) can be performed with different goals for image reduction (downscaling). If the goal is to have an image without aliasing, a lowpass filter must be used. But if the goal is to analyze the texture, or to prepare for morphological analysis at lower resolution, a variety of nonlinear filters can be used before subsampling. The special case of a power of 2 reduction can be implemented very efficiently with word parallel operations. Of most interest are situations where the filtering and subsampling are combined, so that a filtered image at full resolution does not need to be produced before subsampling. When the image resolution is increased (upscaling), it may be desirable to smooth the boundaries to avoid large, visible stair-steps. The details are given below.

Class 3 (binary –> grayscale) is also known as “scale-to-gray.” It is typically used when the image is being downscaled from a high resolution binary scan for viewing on a lower resolution grayscale or color display, and for typical scan and display resolutions, the 3x and 4x reductions are the most useful. We provide fast scale-to-gray reductions for 2x, 3x, 4x, 8x and 16x reduction, all implemented efficiently with lookup tables. For best results at intermediate scale factors, use binary upscaling before fast scale-to-gray reduction. See below for details.

Class 4 (grayscale –> binary), which is the inverse of scale-to-gray, can be called “upscale-to-binary”. It is useful when a lower resolution (e.g., 100 ppi) grayscale image is to be printed on a higher resolution binary device, such as a laser printer. If we were to use pixel replication, the blocks representing the original pixels would be easily visible on the printed page. However, the blocks are much less noticeable if the edges are smoothed, using an interpolated grayscale scaling routine followed by binarization. See below for details.

Grayscale Image Scaling

We describe different methods for scaling a grayscale image, using a general (float) scaling factor that may be either less than 1 (subsampling; downscaling) or greater than 1 (oversampling; upscaling). Implementations are provided for general anisotropic scaling (two independent scaling factors) on 8 bpp grayscale images, as well as on 24 bpp color images. The latter simply requires three independent scalings on the RGB color parts, and is often performed most efficiently one destination pixel at a time.

How do you scale a grayscale image?

In the following, we are assuming that a scaling factor S is used, and that when S is larger than 1.0, the image is magnified (and the dest pixels are smaller than the source pixels), and when S is smaller than 1.0, the image is reduced (and the dest pixels are larger than the source pixels). In the actual implementations, we do not assume isotropic scaling, and provide two scaling factors: S_x and S_y.

Sampling

The simplest scaling method uses sampling. If the image is reduced, we call it subsampling; if the image is enlarged it is replicative sampling. While this method is fast, it gives relatively poor results for both situations.

If the image is reduced, subsampling produces aliasing by the Nyquist theorem. Here’s a simple illustration. Suppose the image consists of alternating light and dark pixel columns, and you subsample with a scale factor of 0.25. You are choosing pixels from every fourth pixel column. Every pixel you choose will be either light or dark, depending on where you start. The high frequency signal has entirely disappeared in the subsampled version. Now suppose the scale factor is 0.24, the first column you pick is dark, and you choose the column integer by truncating the floating point value. The second column you pick will be at 1/0.24 = 4.17 pixels, which is rounded to 4, so it will also be dark. The third will be at 8.33; rounded to 8 is a dark column. And so it continues, with the fourth at 12.5, the fifth at 16.67, and the sixth at 20.83, all dark columns. But the seventh, at 25, will be a light column. The next 5 columns will be also be light, until you get to the thirteenth, at 50.0, which is another dark column. Etc. You have a signal with a periodicity of 12 in the subsampled image. Nothing like this existed in the original. The low-frequency signal in the subsampled image, which corresponds to a periodicty of 50 pixels in the original, appeared through aliasing. To remove the aliasing, it is necessary to remove frequencies in the image whose periodicity is less than twice your sample spacing, because signals from those higher frequencies are aliased down into your reduced bandwidth. So here’s the general rule to remove those high frequencies and avoid aliasing: Use a lowpass filter before subsampling.

If the image is enlarged by a large factor, pixel replication will give a blocky appearance. Each pixel will be magnified into a large block of pixels. Sharp edges will be enlarged, and lines that are nearly horizontal or vertical will have a stair-step appearance at their edges.

Area mapping (or area averaging) and lowpass filtering

When an image is scaled, each dest pixel will partially or completely cover one or more source pixels. In area mapping, the dest pixel value is found by assigning it the average of the source pixels it corresponds to, weighting by the fractional area of each source pixel that it partially (or wholly) covers.

Strict area mapping is fairly expensive, compared to using a lowpass filter that averages entire pixels followed by downsampling. With large upscaling, it gives a result not significantly better than inexpensive replicative sampling. Consequently, it should only be used when downsampling. (Our rule of thumb is to use area mapping for downsampling with a scale factor less than 0.7). With very large downscaling (e.g., a factor less than 0.2), scaling by area mapping (pixScaleAreaMap()) does not give results much better than low-pass filtering followed by subsampling for antialiasing (pixScaleSmooth()). However, for scale factors between about 0.2 and 0.7, it gives significantly better visual results than pixScaleSmooth().

Let’s consider scaling in more detail. Suppose you are enlarging the image, where the scaling factor is much larger than 1. Then most dest pixels cover just a small amount of a single source pixel. Relatively few dest pixels will overlap source pixel boundaries. In this case, the result of area mapping will be nearly identical to that of replicative sampling. Most dest pixels will be assigned the value of a single source pixel, so in this limit, area mapping reduces to subsampling except for the small number of dest pixels that lie across source pixel boundaries, where you get a weighted average of the source pixel values. The appearance, like the case for sampling alone, will be blocky, because you will see each source pixel magnified and with only a little fuzziness around the edge.

At the other limit, where you are doing a large reduction, each dest pixel covers many source pixels. If you take an average of the source pixels, including only the area of each source pixel that is actually covered by the dest pixel, you will get an unaliased and very good estimate of the value each subsampled pixel should have. However, doing this sum is computationally expensive, and the result is not appreciably better than simply doing an average (using an appropriate lowpass filter) followed by subsampling.

As a good rule of thumb, for downscaling with a scale factor less than 0.7, you should use a lowpass filter and then subsample. To prevent aliasing, the size of the lowpass filter kernel on the source image should be approximately the area of the source that corresponds to a single pixel of the dest. The implementation of this approximate filter is straightforward; see pixScaleSmooth(). Better antialiased results are obtained by using strict area mapping, with a filter that is of constant (normalized) height over a rectangular region of the source image that corresponds closely to each dest pixel; see pixScaleAreaMap().

Mip-mapping

Mip-mapping is the name given to the texture mapping method used in graphics (in particular, in games), where a multiresolution pyramid is constructed at power-of-2 scales, and each pixel at an intermediate scale is evaluated by interpolating between the corresponding pixels on the pyramid at resolutions above and below. It is widely used to display textures in graphics for two reasons: (1) the appearance of a texture (a set of neighboring pixels) varies smoothly as the resolution is changed, and (2) hardware to support the pyramids and perform the interpolations in real time is available in high-end graphics cards.

Mipmap scaling can be performed efficiently in the CPU, and we provide an implementation that is used in conjuction with scale-to-gray. For document images with text and sharp edges, mipmap scaling suffers from severe aliasing and should not be used if the quality of the images is important.

Min-max

Morphological transforms are the most important class of non-linear image transforms. Grayscale morphology, even using the van Herk/Gil-Werman method, is relatively expensive if you just want the min or max for each tile in a subsampled image. Rather than performing grayscale morphology on the full resolution image and throwing most of the results away with subsampling, for integer reduction it makes more sense to identify the tiles in the src image that correspond to each dest pixel and compute the min or max (for erosion or dilation) directly.

The function pixScaleGrayMinMax() performs this function for arbitrary (isotropic) downscaling. The speed is about 70 MPix/sec/GHz of source data. For the special case of downscaling by 2x, the function pixScaleGrayMinMax2() is about twice as fast again.

Min-max is a special case of the general rank order downscaler. The problem with the general rank order downscalers is that, except for the min and max values, they require sorting of pixel values. This is relatively expensive: sorting n elements is computationally of order n*log(n). For a 2x2 kernel (which we use here for filtering before a 2x reduction), this isn’t too expensive. A general 2x rank order function pixScaleGrayRank2() allows a choice of the two intermediate rank values in addition to the min and max, but at about 3x the computational cost. For grayscale rank reductions greater than 2x, a sequence of 2x reductions with different ranks can be used to approximate an intermediate rank over the entire (power-of-2) reduction.

Linear interpolation

We describe the implementation(s) of linear interpolation in some detail because it is useful and conceptually simple, and because there exist very efficient implementations for the special cases of 2x and 4x upscaling. The general scaling implementations for linear interpolation of grayscale and RGB images are in the functions pixScaleGrayLI() and pixScaleColorLI(), respectively. They are appropriate for upscaling with a scale factor larger than 1, or for downscaling with a scale factor larger than about 0.7. For scale factors between 0.7 and 2.0, better results are achieved, particularly on orthographically generated images (as opposed to natural scenes) by a small amount of sharpening after scaling.

Implementation of linear interpolation scaling

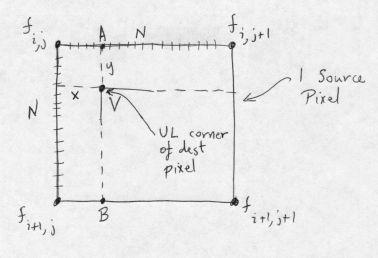
Linear interpolation works as follows. In the figure, f_i,j is the value of the source pixel whose UL corner is at the location [i,j] indicated. Pixel vertices are labelled in standard [row,column] matrix notation. Coordinate values increase as you move down and to the right, which is the standard for image processing. The values of three neighboring source pixels, whose UL corners are on the other corners of the source pixel, are also given. Each source pixel is subdivided into NxN subpixels. We want to determine the value of the dest pixel whose UL corner is at location V. x and y are the coordinates of V, in subpixel units, relative to the UL corner of the source pixel shown. By linear interpolation, using the UL corner values, we get the following values at A and B:

A = (1/N) [(N - x)fi,j + xfi,j+1]

B = (1/N) [(N - x)fi+1,j + xfi+1,j+1]

Then interpolating vertically between A and B:

V = (1/N) [(N - y)A + yB]

  = (1/N2) [(N - x)(N - y)fi,j + x(N - y)fi,j+1 + y(N - x)fi+1,j + xyfi+1,j+1]

This is the normalized result. We choose N = 16 for convenience and sufficient accuracy. It is interesting to compare this to the formula for area mapping at constant scale, used in the rotation algorithm. The filters are identical!

Considerations of efficiency for linear interpolation scaling

The linear interpolation scaling of RGB color images is trivially implemented by pulling out each color component as an image, scaling it as described above, and combining the three scaled color images. However, this suffers from several sources of inefficiency, the biggest of which is the byte-wise extraction and recomposition to form the separate component images. This also requires allocation of the temporary images, and a separate step where the scaled bytes in each component image are again extracted and recombined to form RGB color pixels.

A much better way, which is about 3x faster, is to do the operation whereby each dest RGB pixel is computed from the appropriate source pixels, using separate computations on each component, and extracting the components by shifts and masks. These word-based operations are enabled by our decision to order the RGB components with the MSB leftmost in the 32-bit word, so that we can shift and mask to access and set individual components, without regard for the endian-ness of the hardware. For example, you will see the general color linear interpolation scaling operation in scaleColorLILow() as a direct analog of the grayscale version scaleGrayLILow(), opened up to operate on each component.

For special cases such as 2x linear interpolation, the operations can be increased by a factor of more than 10 by unrolling the loop for each 2x2 set of dest pixels, caching two of the four src pixels for use in the next 2x2 block, and using a special case for the last row of src pixels, where interpolation can only be done horizontally. We implement a function to do a single line, so that it is relatively easy to combine linear interpolation scaling with binarization (either thresholding or dithering). You can see all the byte GETting and SETting for 2x LI in scaleGray2xLILineLow(). We also have a similar 4x LI function, scaleGray4xLILineLow().

These two unrollings — color and destination blocks — can be combined. To get efficient color 2x scaling with linear interpolation, we play the same trick as with the general case: take the grayscale 2x LI function and unroll it further to handle each of the color components, generating the destination pixels on the fly. It’s all laid out in scaleColor2xLILineLow(). I haven’t done the analogous unrolling for 4x color LI scaling; if you need it, the implementation is straightforward.

You can judge whether these efficiency hacks are worthwhile from the computational speed. Here are the times in seconds for four of the functions, on an 8 M RGB color image upscaled by 2x, so that there are 32 M RGB destination pixels (128 MB), using a 2.8 GHz P4 with enough memory to avoid disk paging:

Linear Interpolation Speeds

Linear Interpolation Method	Time (sec)
general LI color	2.4
general LI color using 3 x (general LI gray)	5.4
2x LI color	0.18
2x LI color using 3 x (2x LI gray)	0.7

The salient efficiency results for LI scaling are:

1. it’s important to code the color case up specially (and not use grayscale LI scaling on each component separately),

2. there are huge savings for special scaling factors like 2x for both color and gray, and

3. the extra work to do this is relatively small.

The other basic conditions on LI scaling are:

1. do not use for scale factors below 0.7 because of aliasing problems and

2. for scale factors below about 2.0, best results are obtained by following the LI with a small amount of sharpening.

See pixScale() for a high-level implementation of scaling that selects the operations based on the scale factor.

Binary Image Scaling

The high-level call pixScale() dispatches general scaling to binary, grayscale or color procedures, depending on the depth of the PIX. All these general scaling functions have two scaling parameters, one for horizontal and one for vertical. Scaling is isotropic when these two factors are equal, and anisotropic otherwise.

Consider now binary scaling, and imagine that the scaling is isotropic. There are two cases: the scaling factor(s) can be either greater than 1 (upscaling) or less than 1 (downscaling). As mentioned above, with grayscale images one should use linear interpolation with upscaling, and for downscaling it’s best to use a lowpass filter before subsampling. For binary images, we simply replicate pixels when upscaling. When downscaling binary images, there are three choices:

1. You can downscale by simple subsampling, and take your chances with aliasing.

2. You can apply a lowpass filter before subsampling, which for binary images could be a thresholding function implementing a rank order filter.

3. You can save some of the high resolution information by using a lowpass filter followed by subsampling to convert to a grayscale image at low resolution.

Arbitrary binary rescaling

First, we describe the process for upscaling by replication or downscaling by simple subsampling, in the case of arbitrary scale factors. For further details, consult the source code in scaleBinaryLow() in scalelow.c. We iterate through the destination. Two one-dimensional arrays are set up so that we can quickly find the horizontal and vertical indices of the source pixel corresponding to each pixel in the destination. For downscaling, this will be a different source pixel for each dest pixel, and we set the dest pixel if the source pixel is set. For upscaling, we only check each source pixel once, and if set, we set all the corresponding dest pixels in the row. Once a dest row is complete, we replicate it as many times as are required by the vertical index array.

The situation where the scale factor is arbitrary is relatively inefficient, because we have to read and write individual binary pixels in the source and destination images, respectively. The efficiency can be greatly improved for the special case where the scale factor is a power of 2.

Special case: power-of-2 binary expansion

Consider the situation with a power-of-2 binary replicative expansion. For example, with 2x expansion, we take a byte corresponding to 8 pixels, use this as an index in a 256-entry LUT of 16-bit words, each of which has each bit in the input byte repeated. After the output raster line that has a 2x horizontal expansion has been computed, it is copied again to the destination to give the 2x vertical expansion. Other power-of-2 factors (4, 8, etc.) are computed in a similar way. We use LUTs that have no more than 256 entries throughout, because they are extremely fast. If you want to guild the lily, you will find that 16-bit tables are even faster with most caches. The high-level functions are in binexpand.c and the low-level work on the pixels is all done in binexpandlow.c.

Special case: 2x binary reduction

The situation with power-of-2 binary rank-order filtered reduction is a little more complicated. Remember, we can do this for arbitrary rank order rectangular filters using the pixBlockrank() function, although, because of its generality, it is considerably slower than the special functions we describe here. The high-level functions are in binreduce.c and the pixel pushing is all done in binreducelow.c. See the source code for details and clarification of the description here.

Consider first 2x subsampling without filtering. If you want to use a LUT, there are two ways to do it. With an 8-bit LUT, you can store in the table the 4 bits (say, bits 0, 2, 4, and 6) that you are taking for each 8 bits (0 - 7) in. This is very fast, but you can get some improvement by masking out all the odd bits in a 32-bit word, and then ORing this masked word with itself, left-shifted by 7 bits. That puts the first 8 even bits (0, 2, ... 14), which will be bits (0, 1, ... 7) in the reduced image, into the first byte. There, they are in bit order (0, 4, 1, 5, 2, 6, 3, 7). An 8-bit LUT is then used to permute them to the normal order (0, 1, ... 7) in the output byte. Likewise, the second set of 8 even bits land in the third byte, and must be permuted in the same way. This is performed on even raster lines; odd raster lines are ignored in the 2x reduction.

Either of these subsampling methods can be pre-filtered. But it is only necessary to get the filtered results at the pixels that will be subsampled, because the other pixels are discarded at subsampling. The main reason these operations are so fast is that it is not necessary to generate a full filtered image before subsampling. Now, these are binary images, so we must use a convolution filter and apply a threshold on the result. For a 2x reduction, it makes sense only to use the 4 pixels in each 2x2 square, from which a single pixel will be chosen. The filter weights on these 4 pixels should be equal, so we simply count the ON pixels in each 2x2 square and apply a threshold on the count. How do we efficiently get the result of this thresholded count into a specified pixel in each 2x2 square? The solution, which was found in 1991, is very simple and can be found in the appendix of the paper, Image Analysis using Threshold Reduction.

Two examples will give you the general idea. Suppose we want a threshold of 1 (rank value of 1/4), which means that if any pixels in a 2x2 square are ON, we get an ON pixel in the upper-left corner of this 2x2 square. If we do a morphological dilation using a 2x2 structuring element with center in the lower-right corner, we will get the correct pixel in the upper-left corner, and we will also get the shift-invariant filtered results in the other 3 pixels in each 2x2 square. We could then subsample any of these pixels, because they all have been filtered. Obviously, we have done too much work! Because we are only sampling the upper-left pixels in each 2x2 square, to get the information about the other 3 pixels there, OR each word with itself left-shifted by one pixel, and follow this by a vertical OR of each word on odd raster lines with the word above it, storing the result in the words on even raster lines. With three 32-bit ORs, we thus generate 16 filtered pixels for subsampling. The filtering turns out to be much faster than the subsampling! The second example implements a threshold of 4 (rank value of 4/4), which means that all pixels in a 2x2 square must be ON for the upper-left pixel to be turned on. Again this can be implemented morphologically with an erosion, this time using a 2x2 structuring element with the center in the upper-left corner. And again, more efficiently, this can be implemented by logically performing three ANDs, in the same way that we used three ORs for threshold 1.

What about threshold levels 2 and 3? These are only slightly more complicated to implement with bit-logical operations. We need to perform both a horizontal AND and vertical OR, and a horizontal OR and a vertical AND. Then, taking the OR of these two results gives a threshold of 2, whereas taking the AND gives a threshold of 3. You can demonstrate that this works by setting up a logic table consisting of all 16 possible 2x2 binary pixels, and applying these operations. Consult the paper for a proof.

As would be expected because of the dilation, reduction using a threshold of 1 makes the image darker. Reduction using a threshold of 4 makes it much lighter. Reduction with threshold 2 appears to preserve the apparent darkness of the original image, as might be expected from a median filter (rank order of 2/4 = 0.5).

A cascade of successive 2x threshold reductions is very useful for document image analysis, because it combines morphological filtering with reduction in such a way as to select textural qualities at different scales. Texture in a binary image can be thought of as the statistical distribution of neighbor pixels of the opposite color. Although morphological operations such as the opening or hit-miss are typically considered to be shape-filtering, they can also be used to filter texture. This is an interesting story, and you are referred to the 1991 papers Image Analysis using Threshold Reduction and Multiresolution morphological approach to document image analysis for simple examples with document images.

Binary to Gray Downscaling (“scale-to-gray”)

Scanners typically scan binary images at 300 to 400 ppi (pixels/inch), but displays are typically around 80 ppi grayscale. How do you make a binary scanned image readable on a grayscale (or color) display? If you display it at full resolution, the width of an 8.5 inch page is larger than the display, so that horizontal scrolling is required to read each line. The letters are also about 4 times larger on the screen than they were on paper. Consequently, it is desirable to reduce the image to fit on a display.

You have the choice of making a binary or a grayscale reduced image. In both cases, subsampling is required, and the methods described above for avoiding aliasing apply here as well. Namely, you should apply a lowpass filter before subsampling. There are many ways to do this, using either linear or nonlinear filters. But the net result will have a much poorer appearance if you make a binary reduced image. In fact, a page of 8 pt font, scanned binary at 300 ppi and reduced 4x to 75 ppi binary, will be essentially unreadable on a screen, regardless of the lowpass filter used. However, if you use a 4x scale-to-gray reduction filter, where each reduced dest pixel is taken to be the average of the 16 corresponding source pixels, the text will be readable, though difficult. (For such small type, you should use a 3x scale-to-gray reduction filter.)

The implementation of Nx scale-to-gray requires taking each NxN pixel block in the binary source and converting it to a single gray pixel with correct normalization. Consider N=4. The sum of the 16 binary source pixels can take on 17 different values, from 0 to 16. This range must be mapped to 255 to 0. The value inversion is due to the convention that a binary black pixel (value = 1) gets mapped to black (value = 0) in a grayscale image. (The gray values increase with the lightness of the pixel.)

So for each dest pixel, we use a table to find the sum of black pixels in the NxN corresponding source pixels, and then use another table to map that sum to the output grayscale value. The 4x scale-to-gray is very simple, because 8-bit lookup tables can be used to accumulate the sums in two adjacent dest pixels simultaneously. For each possible set of 8 adjacent source pixels, the sums of the first and last 4 are packed separately in different bytes of the table word. These words are then summed for 4 adjacent source rows, giving the sums for the two dest pixels. The second lookup table is then used twice to convert each sum to the final 8 bpp dest pixel value. The 3x scale-to-gray is more complicated because the inner loop of an efficient implementation computes 8 dest pixels from 3 rows of 24 source pixels. There is some additional shifting and masking, but the basic algorithm is the same, and again requires two different lookup tables.

We provide high-level interfaces for the following integer reduction values for scale-to-gray: 2x, 3x, 4x, 8x and 16x, in scale.c. For images scanned at 300 ppi binary, 3x scale-to-gray generates a 100 ppi grayscale image, which is comfortable to read on most computer screens. Likewise, for images scanned at 400 ppi binary, 4x scale-to-gray produces a correspondingly readable image. As usual, the low-level functions, that only take array pointers, ints and floats, and do all the bit munging, are provided in scalelow.c.

Because of the importance of creating good downscaled grayscale renderings of high resolution binary images, we also provide a high-level interface for scaling of binary to gray with an arbitrary isotropic scale factor. The function is pixScaleToGray(), and the source code describes the approach in some detail. Here is a summary of the problem. Binary images have sharp edges, so they intrinsically have very high frequency content. To avoid aliasing, they must be low-pass filtered, which tends to blur the edges. How can we keep relatively crisp edges without aliasing? The trick is to do binary upscaling followed by a power-of-2 scale-to-gray, rather than doing a power-of-2 scale-to-gray followed by rescaling in grayscale. For larger reductions, where you don’t end up with much detail, you can use binary downscaling before the scale-to-gray, to reduce the amount of computation. And for very large reductions, the scale-to-gray operation can be done first with little loss in quality of the result.

The general function is implemented with the goal of getting high quality reduced grayscale images with relatively little computation:

1. For scalefactors > 1/8, do binary upscaling before scale-to-gray.

2. For scalefactors between 1/16 and 1/8, do binary downscaling before scale-to-gray.

3. For scalefactors < 1/16, do scale-to-gray (16x) first, and then grayscale downscaling.

Gray to binary upscaling (“scale-to-binary”)

As mentioned above (Class 4), it is useful to convert a low resolution grayscale or color image to a higher resolution binary image for printing, as most printers have binary output at the pixel level. (They can print gray appearance by applying a halftone mask to the grayscale or color image.)

To achieve smooth results, this should be implemented using an interpolated grayscale scaling function that is followed by binarization. Further, to limit the amount of allocated memory, it is best not to generate the full higher resolution grayscale or color image, but instead, use a minimum-sized buffer from which the binary pixels are immediately produced. Such an implementation is quite tricky for arbitrary size expansion, but it is relatively simple for 2x and 4x expansions. Fortunately, these two handle many common requirements.

Binarization can be produced by thresholding, error diffusion dithering, or ordered dithering using a halftone cell. For images of text, thresholding is fine, but if there are gray image regions, the results are far better with some type of dithering. Further, depending on the printer, a gamma factor should be applied to the grayscale image before dithering an image area, and for typical write-black laser printers, a gamma factor of between 2.0 and 2.7 is typically used to lighten the resulting printed image.

We provide two integrated scale-to-binary operations, with 2x linear interpolated scaling followed by binarization, in scale.c. The upscaled grayscale image pixels are kept in a buffer of not more than 3 lines, and binarization is performed by either thresholding or error-diffusion dithering. Low-level functions are in binarizelow.c.

We also provide two integrated scale-to-binary operations, with 4x linear interpolated scaling followed by binarization. The upscaled grayscale image pixels are generated 4 lines at a time, for binarization by either thresholding or error-diffusion dithering. For thresholding, the buffer size is 4 lines, and for error-diffusion dithering the buffer size is 5 lines. The source is also in scale.c, with the lowest level functions in binarizelow.c.

Fast scaling with depth change

And finally, there are functions that are useful if you have RGB images but must analyze them in grayscale or binary, often at reduced resolution. There are different ways these functions can be implemented, and the main consideration is to do it fast and not worry too much about small distortions. As always in such situations, it is important not to do anything except for subsampling on the full resolution image.

We have implemented three of these very simple functions, the choice of which depend on the src and dest depth, all for isotropic integer reduction factors. For downscaling RGB to grayscale, use pixScaleRGBToGrayFast(). For downscaling RGB to binary, use pixScaleRGBToBinaryFast(). And for downscaling grayscale to binary, use pixScaleGrayToBinaryFast().

Summary of scaling functions in leptonica

There is a considerable variety of image scaling functions that can be found in Leptonica, so it is useful to summarize them. These functions are found in seven files:

• scale.c and scalelow.c. These have arbitrary scaling (up or down) by nearest pixel sampling. For grayscale and color, you get three additional choices. You can use linear interpolation for upscaling and moderate downscaling; you can use area mapping for downscaling with a scale factor less than 0.7; and you can use lowpass filtering followed by subsampling for downscaling with a scale factor less than 0.7. There are fast functions for reducing both scale and bpp together. You can use downscale scale-to-gray, with special cases for 2x, 3x, 4x, 8x and 16x reduction, and upscale scale-to-binary, with special cases for 2x and 4x expansion. There is also rank downscaling for grayscale by factors of 2, as well as min and max grayscale reduction by integer factors.

• binreduce.c and binreducelow.c. There are two types of 2x reduction of binary images: subsampled and rank-filtered. We also provide a cascade of 2x rank-filtered reductions.

• binexpand.c and binexpandlow.c. These have fast power-of-2 expansion of binary images.

• binarizelow.c. This handles low-level thresholding and dithering that are an intrinsic part of 2x and 4x upscale gray-to-binary.

The high-level functions, and the types of images that they operate on, are given in the table below. The scaling “type” is one of the following:

• “interp”: interpolating

• “interp*”: interpolating on color and grayscale; sampling on binary

• “sampl”: sampling without interpolation or lowpasss filtering

• “antialias”: low-pass filtering followed by sampling

• “areamap”: accurate summation of src subpixels for each dest pixel

• “minmax”: takes the min or max of components within square set of src pixels

• “scaletogray”: conversion of binary to lower resolution 8 bpp gray

• “rank”: rank filtering before sampling, only on 2x binary and gray reduction

• “replicate”: replicative expansion, by integer factors

We give two tables. The first is for scaling operations that preserve the depth (except where a colormap exists and is removed).

Name                     src depth w/o cmap   depth w/ cmap   type          scale factor
==========================================================================================
pixScale                 1, 2, 4, 8, 16, 32   2, 4, 8         interp*       arbitrary
pixScaleLI               2, 4, 8, 32          2, 4, 8         interp        arbitrary
pixScaleColorLI          32                   -               interp        arbitrary
pixScaleColor2xLI        32                   -               interp        2x expansion
pixScaleColor4xLI        32                   -               interp        4x expansion
pixScaleGrayLI           8                    -               interp        arbitrary
pixScaleGray2xLI         8                    -               interp        2x expansion
pixScaleGray4xLI         8                    -               interp        4x expansion
pixScaleBySampling       1, 8, 16, 32         2, 4, 8         sampl         arbitrary
pixScaleSmooth           2, 4, 8, 32          2, 4, 8         antialias     less than 0.7
pixScaleAreaMap          2, 4, 8, 32          2, 4, 8         areamap       less than 0.7
pixScaleAreaMap2         2, 4, 8, 32          2, 4, 8         areamap       2x reduction
pixScaleBinary           1                    -               sampl         arbitrary
pixScaleGrayMinMax       8                    -               minmax        integer reduction
pixScaleGrayMinMax2      8                    -               minmax        2x reduction
pixScaleGrayRank2        8                    -               rank          2x reduction
pixScaleGrayRankCascade  8                    -               rank          up to four 2x reductions
pixReduceBinary2         1                    -               sampl         2x reduction
pixReduceRankBinary2     1                    -               rank          2x reduction
pixReduceRankBinaryCascade 1                  -               rank          up to four 2x reductions
pixExpandReplicate       1, 2, 4, 8, 16, 32   2, 4, 8         replicate     integer expansion
pixExpandBinary2         1                    -               replicate     power-of-2 expansion
==============================================================================================
               Table of high-level depth-preserving scaling functions

The second table is for scaling operations that do not preserve the depth, such as downscaling binary to gray or upscaling gray to binary.

Name                     src depth w/o cmap   dest depth    type          scale factor
==========================================================================================
pixScaleRGBToGrayFast    32                   8             sampl         integer reduction
pixScaleRGBToBinaryFast  32                   1             sampl         integer reduction
pixScaleGrayToBinaryFast 32                   1             sampl         integer reduction
pixScaleRGBToGray2       32                   8             areamap       2x reduction
pixScaleToGray           1                    8             scaletogray   less than 1.0
pixScaleToGray2          1                    8             scaletogray   2x reduction
pixScaleToGray3          1                    8             scaletogray   3x reduction
pixScaleToGray4          1                    8             scaletogray   4x reduction
pixScaleToGray8          1                    8             scaletogray   8x reduction
pixScaleToGray16         1                    8             scaletogray   16x reduction
pixScaleToGrayMipmap     1                    8             scaletogray   less than 1.0
pixScaleGray2xLIThresh   8                    1             interp        2x expansion
pixScaleGray2xLIDither   8                    1             interp        2x expansion
pixScaleGray4xLIThresh   8                    1             interp        4x expansion
pixScaleGray4xLIDither   8                    1             interp        4x expansion
==============================================================================================
           Table of high-level scaling functions that do not preserve depth

Several things should be noted about the tables:

• The depths of the source image that are supported by the operation are given both for images that do not have a colormap and for images that have one.

• Full RGB color images are stored with 32 bpp. We are, however, only using three 8 bit color components for RGB color (i.e., we ignore the A byte, which is typically used for blending two images).

• In the case of interpolative and area-map antialiased scaling on images with a colormap, the destination image depth is either 8 (gray) or 32 (RGB), depending on the colormap, which is removed.

• There is no redundancy in low-level implementations. For example, if the input image is binary, both pixScale() and pixScaleBySampling() call pixScaleBinary(), which calls scaleBinaryLow() to handle arbitrary scaling by sampling on binary images.